lunes, 14 de diciembre de 2015
Tasa Relacionada
Se trata de un problema en el que se proporciona la tasa de variación de al menos una variable de la función y en el problema se necesita buscar la otra tasa de variación.
También hay ciertas reglas simples para resolver estos problemas:
Considere que f(a) sea una función con dos variables a y b, las cuales cambian con el tiempo y la tasa de variación de a es dada con el tiempo, es decir, da/dt
1) En primer lugar, encontrar la derivada de f(a), es decir, f'(a)
2) Ponga el valor de a en la ecuación
3) Entonces multiplíquelo con da/dt para obtener db/dt
Aplicar las reglas en un ejemplo proporcionará una mejor comprensión:
Suponga que la pregunta dada dice lo siguiente:
Se está bombeando aire a un globo esférico de 4 cm de radio a 5 cm3 / seg.
Entonces,el ritmo de cambio del radio del globo necesita ser calculado.
Se puede observar que el radio y el volumen son las variables de las funciones correspondientes.
dv/ dt es dada y es igual a 5 cm3/seg y dr/dt necesita encontrarse.
Como V= 4 r3 / 3.
Diferenciando ambos lados, se obtiene . dV/dt=4π r 2 dr/dt
Ahora sustituyendo el valor de en esta ecuación, se obtiene dr/dt= 7/64π cm /seg.
Optimizacion
La optimización se refiere al tipo de problema que se ocupa de la determinación de la forma más apropiada para realizar cierta tarea. Con el fin de resolver estos problemas, se calculan los valores mínimos y máximos de la función. Estos incluyen encontrar la distancia mínima para llegar a un punto, el costo mínimo para hacer determinada operación, etc. La función cuyo máximo o mínimo necesita determinase por lo general está sujeta a ciertas restricciones que deben tomarse en cuenta.
Estos problemas son diferentes a los problemas utilizados para encontrar los valores mínimos o máximos locales. Los Problemas de optimización sólo se ocupan de los valores máximos o mínimos que una función puede tomar y no del mínimo o máximo en un intervalo. Es decir, la optimización busca el mínimo o máximo global (absoluto) y no el local. El mínimo o máximo absoluto es el mayor entre el mínimo o máximo local, respectivamente.
Puede haber casos, donde el mínimo o máximo global no existe para una función. En estos el dibujo de la gráfica para la función correspondiente puede ayudar en gran manera.
Hay algunos pasos que deben seguirse con el fin de desglosar un problema de optimización:
1). Lo primero y más importante es identificar las vairables y constantes de la función. Esto ayuda a determinar la parte de la función que será minimizada o maximizada.
2). Escribir la fórmula adecuada para la función particular, para lo cual tenemos que calcular el mínimo o máximo.
3). Ahora, la fórmula será escrita en términos de una sola variable, es decir, f®.
4). Establezca la diferenciación de f® a 0, f ‘® = 0, y resuelva a través de observar todas las limitaciones y otros valores críticos para encontrar los valores extremos.
Cálculo De Aproximaciones Usando La Diferencial
En cálculo, la diferencial representa la parte principal del cambio en una función y = ƒ(x) con respecto a los cambios en la variable independiente. La misma diferencia se define por una expresión de la forma dy = {dy}{dx}\dx como si el derivados dy/dx representa el cociente de una cantidad dy por una cantidad dx. También se escribe df(x) = f’(x)dx. El significado preciso de tales expresiones depende del contexto de la aplicación y el nivel requerido de rigor matemático. En los tratamientos modernos matemáticos rigurosos, las cantidades dy y dx son simplemente más real variables que puede ser manipulado como tal. El dominio de estas variables pueden tener un significado geométrico particular, si el diferencial se considera un particular forma diferencial, o la importancia de análisis, si el diferencial se considera como una aproximación lineal al incremento de una función. En las aplicaciones físicas, las variables dx y dy a menudo, deben ser muy pequeñas (“infinitesimal”). El diferencial fue introducido por primera vez a través de definiciones intuitivas o heurístico Gottfried Wilhelm Leibniz, que pensaba de la diferencia dy como lo infinitamente pequeño (o infinitesimal) cambio en el valor y de la función, que corresponde a un cambio infinitamente pequeño dx en el argumento de la función x. Por esa razón, la razón instantánea de cambio de y con respecto a x, que es el valor de la derivados de la función, se denota por la fracción {dy}{dx} en lo que se llama el Leibniz notación para los derivados. El cociente dy/dx es, por supuesto, no lo infinitamente pequeño, sino que es un número real. El uso de los infinitesimales en esta forma fue muy criticado, por ejemplo, el famoso panfleto “El Analista” por el obispo Berkeley. Augustin-Louis Cauchy (1823) se define la diferencia, sin apelar a la teoría atómica de los infinitesimales de Leibniz. En cambio, Cauchy, tras D’Alembert, se invierte el orden lógico de Leibniz y sus sucesores: el derivado de sí mismo se convirtió en el objeto fundamental, que se define como un límite de los cocientes de diferencia, y los diferenciales se definieron a continuación, en términos de la misma. Es decir, uno era libre de definir el diferencial dy por una expresión dy = f’(x)dx en el que dy y dx son simplemente nuevas variables tomando finitos valores reales, no fija los infinitesimales como lo habían sido por Leibniz.
Criterios de la segunda derivada
El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Se basa en el hecho de que si la gráfica de una función  es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.
 es convexa en un intervalo abierto que contiene a
es convexa en un intervalo abierto que contiene a  , y
, y  debe ser un mínimo relativo de
debe ser un mínimo relativo de  . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a
. De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a  y
y  debe ser un máximo relativo de
debe ser un máximo relativo de  .
.Teorema
Sea  una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
 una función tal que
una función tal que  y la segunda derivada de
y la segunda derivada de  existe en un intervalo abierto que contiene a
existe en un intervalo abierto que contiene a 
- Si
 , entonces
, entonces  tiene un máximo relativo en
tiene un máximo relativo en  .
. - Si
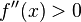 , entonces
, entonces  tiene un mínimo relativo en
tiene un mínimo relativo en  .
.
- Si
 , entonces el criterio falla. Esto es,
, entonces el criterio falla. Esto es,  quizás tenga un máximo relativo en
quizás tenga un máximo relativo en  , un mínimo relativo en
, un mínimo relativo en  o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
Teorema de valor medio
En cálculo diferencial, el teorema de valor medio (de Lagrange), teorema de los incrementos finitos, teorema de Bonnet-Lagrange o teoría del punto medio es una propiedad de las funciones derivables en un intervalo. Algunos matemáticos consideran que este teorema es el más importante del cálculo (ver también el teorema fundamental del cálculo integral). El teorema no se usa para resolver problemas matemáticos; más bien, se usa normalmente para demostrar otros teoremas. El teorema de valor medio puede usarse para demostrar el teorema de Taylor ya que es un caso especial.
Analisis de la Variacion de Funciones
Análisis de la Variación de la Función


Cuando la variación total de cualquier función particular es finita, en ese caso, esa función se conoce como Función de Variación Acotada, que puede ser abreviada como función BV (Bounded Variation por sus siglas en inglés). El gráfico correspondiente de la función BV se dice entonces que se comporta bien en un sentido preciso. La función BV tiene amplias aplicaciones en el campo de las matemáticas, y es utilizada en algunos de los teoremas más importantes, tal como son los Teoremas de Fourier. En el caso de la funciones continuas que contienen sólo una variable, la variación acotada implica la distancia finita cubierta por un punto a lo largo del eje y. Otra clasificación establece que las funciones de variación acotada, tienen la propiedad de intervalo cerrado, son las funciones que se pueden establecer como la diferencia entre dos monótonas acotadas.
La variación Acotada de una función determinada en el intervalo [x, y] puede ser establecida como
Donde S es el conjunto acotado
La variación resulta ser infinita si el conjunto no es acotado. El supremo de S puede ser llamado también como Variación Total o sólo la variación de f y se denota como V (f; x, y) o simplemente V (x).
Existen ciertos teoremas que pueden ser útiles para el análisis de la variación de la función:
1). Si en el conjunto [x, y], la función está incrementando, en ese caso, es la función de variación acotada en el conjunto [x, y] y consecuentemente V [g [x, y]] = g(y) – g(x).
2). Si en el conjunto [x, y] la función es constante, entonces es la función de variación acotada en el conjunto [x, y] y entonces V [g [x, y]] = 0.
Por ejemplo, la función g(r) = c es una función de variación acotada constante en el intervalo [x, y].  | g (ri) – g (ri - 1)| = 0 por cada partición del conjunto [a, b]. Por tanto, V (g, [x, y]) = 0.
| g (ri) – g (ri - 1)| = 0 por cada partición del conjunto [a, b]. Por tanto, V (g, [x, y]) = 0.
3) En el conjunto [x, y] si, g y f son las funciones de variación acotada y c es constante, en ese caso
a). g es una función de variación acotada en el intervalo [x, y].
b). g es una función de variación acotada en cada subintervalo cerrado del intervalo [x, y].
c). cg es también una función BV en el conjunto [x, y].
d). g + f y g –f son BV en el conjunto [x, y]
e). gf es también BV en el conjunto [x, y].
Algunos datos más útiles acerca de estas funciones especiales se pueden establecer como que una función de variación acotada se puede expresar también por la divergencia de 2 funciones crecientes.
Del mismo modo, todas las funciones totalmente continuas son de naturaleza BV, sin embargo, no es necesario que todas las funciones continuas BV deban ser totalmente continuas.
La función f puede ser considerada como BV en el conjunto [x, y] si, la derivada de f se encuentra acotada en [x, y]. Además, cuando dos funciones variación acotada se multiplican entre sí, entonces la resultante es también una función de variación acotada.
Teorema de Rolle
El teorema de Rolle demuestra la existencia de un punto interior en un intervalo abierto para el cual la derivada de una función derivable se anula cuando el valor de ésta en los extremos del intervalo es el mismo. Es generalizado mediante el teorema del valor medio, del que este es un caso especial. Es uno de los principales teoremas en cálculo debido a sus aplicaciones.
Se puede enunciar de la siguiente manera,
Se sabe que existen tres posibilidades, o bien la función que consideramos es constante, o bien tiene algún punto x donde el valor de la función es mayor o bien este valor es menor que en los extremos. Para el primer caso es trivial que en algún punto la función tiene derivada nula (en la definición de derivada el cociente incremental es cero).
|
Pendiente dela recta tangente a una curva
La recta tangente a una curva es la que coincide con la curva en un punto y con la misma derivada, es decir, el mismo grado de variación.
El conocimiento de la recta tangente permitirá resolver problemas sencillos: en primer lugar, se podrán encontrar tangentes a cualquier función que se pueda derivar, en cualquier punto, como se observa en el primer ejemplo resuelto a continuación. En segundo lugar y como se puede ver en el segundo ejemplo, se puede utilizar como condición en problemas más complejos.
La recta y=m⋅x+b es tangente a la curva f(x) si cumple los siguientes requisitos:
- Pasa por el punto de tangencia:
(a,f(a)) - Tiene el mismo pendiente (mismo valor de la derivada) que la curva en el punto de tangencia:
m=f′(a)
sábado, 31 de octubre de 2015
SUCESIÓN
Una sucesión se va aproximando hacia un punto llamado límite. Si una sucesión tiene límite, se dice que es una sucesión convergente, y que la sucesión converge o tiende al límite. En caso contrario, la sucesión es divergente.
La definición significa que eventualmente todos los elementos de la sucesión se aproximan tanto como queramos al valor límite. La condición que impone que los elementos se encuentren arbitrariamente cercanos a los elementos subsiguientes no implica, en general, que la sucesión tenga un límite.
Se denota:

lunes, 5 de octubre de 2015
DIVERSOS METODOS PARA LAS GRAFICAS
Una función con una variable dependiente y otra independiente se puede representar gráficamente en un eje de coordenadas y abscisas correspondiendo el valor de cada variable a la posición en los ejes. Normalmente se utiliza la variable 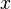 para el eje de abscisas y la variable
para el eje de abscisas y la variable  para el eje de ordenadas.
para el eje de ordenadas.
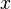 para el eje de abscisas y la variable
para el eje de abscisas y la variable  para el eje de ordenadas.
para el eje de ordenadas.
Para dibujar, construir o representar la gráfica de una función f se pueden seguir los pasos siguientes:
- Buscar el dominio de la función, Dom f(x)
- Se detectan aquellos valores x reales en que f sea discontinua, es decir, aquellos que no estén definidos en el dominio, y se procede a estudiar los limites cuando x tiene a x por la izquierda y por la derecha. De este modo, si x es un punto aislado y no un intervalo, se puede deducir hacia dónde tiende la función cuando pasa cerca del punto x.
- Buscar los límites cuando x tiende a infinito o menos infinito, para averiguar cuándo en el eje de abscisas se tiende al resultado del límite.
- Estudio de la monotonia. Calculando la primera derivada f'(x) e igualándola a cero, se obtienen los posibles candidatos a extremos de la función. Luego se procede a determinar si f(x) es creciente o decreciente entre dos puntos extremos.
- Se estudia la curvatura de f, igualando a cero esta vez la segunda derivada f(x), obteniéndose los posibles puntos de inflexion. Se estudia el signo en la f(x) en los intervalos, y así, sea x uno de estos puntos:
-
- Si f(x) es negativa, entonces f(x) es concava.
- Si f(x) es positiva, entonces f(x) es convexa.
FUNCIÓN, REPRESENTACIÓN, RELACIÓN ENTRE CONJUNTOS
FUNCION
Una función es una relación entre dos variables, de forma que a cada valor de la variable independiente  , le asocia un único valor de la variable dependiente
, le asocia un único valor de la variable dependiente  , que llamaremos imagen de
, que llamaremos imagen de  . Decimos que y es función de
. Decimos que y es función de  y lo se representa por:
y lo se representa por:
REPRESENTACION
Es un
tipo de representación de datos,
generalmente numéricos,
mediante recursos gráficos (lineas,vectores, superficies o símbolos), para que se
manifieste visualmente la relación matemática o correlación estadística que
guardan entre sí. También es el nombre de un conjunto d puntos que
se plasman en coordenadas cartesianas y sirven para analizar el comportamiento de un
proceso o un conjunto de elementos o
signos que permiten la interpretación de un fenómeno. La representación gráfica
permite establecer valores que no se han obtenido experimentalmente sino
mediante la interpolacion (lectura
entre puntos) y la extrapolacion (valores
fuera del intervalo experimental).
RELACIÓN ENTRE CONJUNTOS
Relación es la correspondencia de un primer conjunto, llamado Dominio, con un segundo conjunto, llamadoRecorrido o Rango, de manera que a cada elemento del Dominio le corresponde uno o más elementos del Recorrido o Rango.
También debemos agregar que toda ecuación es una Relación, pero no toda ecuación es una Función.
Todas las Relaciones pueden ser graficadas en el Plano Cartesiano.
Dados dos conjuntos A y B una relación definida de A en B es un conjunto de parejas ordenadas (par ordenado) que hacen verdadera una proposición; dicho de otro modo, una relación es cualquier subconjunto del producto cartesiano A x B.
Suscribirse a:
Entradas (Atom)







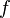 es una
es una ![\ [a, b]](https://upload.wikimedia.org/math/5/f/c/5fc1fbc48b5a353c0095a0f55f520e32.png) ,
, 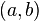 y
y  , entonces:
, entonces: perteneciente al intervalo
perteneciente al intervalo  .
.

