El Criterio o prueba de la segunda derivada es un teorema o método del cálculo matemático en el que se utiliza la segunda derivada para efectuar una prueba simple correspondiente a los máximos y mínimos relativos.
Se basa en el hecho de que si la gráfica de una función 
es convexa en un intervalo abierto que contiene a 
, y 
debe ser un mínimo relativo de . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a y debe ser un máximo relativo de .
es convexa en un intervalo abierto que contiene a , y debe ser un mínimo relativo de . De manera similar, si la gráfica de una función es cóncava hacia abajo en un intervalo abierto que contiene a y debe ser un máximo relativo de .Teorema
Sea una función tal que 
y la segunda derivada de existe en un intervalo abierto que contiene a 
una función tal que y la segunda derivada de existe en un intervalo abierto que contiene a - Si
, entonces tiene un máximo relativo en 
. - Si
, entonces tiene un mínimo relativo en .
- Si
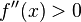, entonces el criterio falla. Esto es, quizás tenga un máximo relativo en , un mínimo relativo en o ninguno de los dos. Tomar como ejemplo la función f(x) = x³. En tales casos, se puede utilizar el criterio de la primera derivada o el criterio de la tercera derivada.
No hay comentarios.:
Publicar un comentario