Una función con una variable dependiente y otra independiente se puede representar gráficamente en un eje de coordenadas y abscisas correspondiendo el valor de cada variable a la posición en los ejes. Normalmente se utiliza la variable 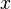 para el eje de abscisas y la variable
para el eje de abscisas y la variable  para el eje de ordenadas.
para el eje de ordenadas.
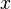 para el eje de abscisas y la variable
para el eje de abscisas y la variable  para el eje de ordenadas.
para el eje de ordenadas.
Para dibujar, construir o representar la gráfica de una función f se pueden seguir los pasos siguientes:
- Buscar el dominio de la función, Dom f(x)
- Se detectan aquellos valores x reales en que f sea discontinua, es decir, aquellos que no estén definidos en el dominio, y se procede a estudiar los limites cuando x tiene a x por la izquierda y por la derecha. De este modo, si x es un punto aislado y no un intervalo, se puede deducir hacia dónde tiende la función cuando pasa cerca del punto x.
- Buscar los límites cuando x tiende a infinito o menos infinito, para averiguar cuándo en el eje de abscisas se tiende al resultado del límite.
- Estudio de la monotonia. Calculando la primera derivada f'(x) e igualándola a cero, se obtienen los posibles candidatos a extremos de la función. Luego se procede a determinar si f(x) es creciente o decreciente entre dos puntos extremos.
- Se estudia la curvatura de f, igualando a cero esta vez la segunda derivada f(x), obteniéndose los posibles puntos de inflexion. Se estudia el signo en la f(x) en los intervalos, y así, sea x uno de estos puntos:
-
- Si f(x) es negativa, entonces f(x) es concava.
- Si f(x) es positiva, entonces f(x) es convexa.

No hay comentarios.:
Publicar un comentario